Tema N°15: Trinomio de la forma x2n+bxn+c y ax2n+bxn+c

Encuentra los números que cumplan con la condición

Trinomio de la forma x2n+bxn+c
El trinomio x2n+bxn+c se factoriza encontrando dos números m, n tales que su suma sea igual a b y su producto sea igual a c. Si c es positivo, los factores tienen el mismo signo. Si c es negativo, los factores tienen signos diferentes. Si estos números no exiten, entonces se dice que el trinomio no es factorizable por este método.
Ejemplos
Trinomio de la forma ax2n+bxn+c
Este tipo de trinomio se diferencia del anterior debido a que el termino al cuadrado (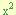 ) se encuentra precedido por un coeficiente diferente de uno (debe ser positivo). Este se trabaja de una manera un poco diferente, la cual detallamos a continuación:
) se encuentra precedido por un coeficiente diferente de uno (debe ser positivo). Este se trabaja de una manera un poco diferente, la cual detallamos a continuación:
- Multiplicamos el coeficiente “a” de el factor “a
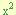 ” por cada termino del trinomio, dejando esta multiplicación indicada en el termino “bx” de la manera “b(ax)”, y en el termino “a
” por cada termino del trinomio, dejando esta multiplicación indicada en el termino “bx” de la manera “b(ax)”, y en el termino “a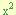 ” de la manera
” de la manera 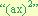 .
.
- Se descompone el trinomio en dos factores binomios cuyo primer termino será la raíz cuadrada del termino
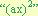 la que seria “ax”.
la que seria “ax”.
- al producto resultante lo dividimos entre el factor “a”, con el fin de no variar el valor del polinomio.
- El signo del primer binomio será el mismo signo que tenga el termino “bx”, el signo del segundo binomio será igual a la multiplicación de los signos de “bx” y de “c”.
- Se buscaran los segundos términos de los binomios según los pasos tres y cuatro del caso del trinomio anterior.
Ejemplos

Factorización trinomio, una ficha interactiva de Daissy_Ospina
liveworksheets.com
liveworksheets.com